Solving the biology literature begins as an exercise in exploring cells as complexities. By copying the way cells change empirically, for example, reproducible patterns can appear in published data accompanied by the rules and first principles that allow cells to operate as complexities. Cells change to solve complex problems by physically becoming the complex solutions. This can involve changing and reproducing thousands of parts and connections existing in millions of cells. Cells accomplish this feat by replacing the recipe of one cell phenotype with that of another. When a “control” cell is given a problem to solve, the cell literally grows into the solution. A changed cell – when widely duplicated by many cells – represents a new cell phenotype with a built-in solution. When going from published data to the phenotype of a changed cell, two guiding principles become the norm: play by the cell’s rules and avoid the “cell changes” produced by the methods.

To solve problems, cells use simple and complex changes in their parts by reconfiguring them into nested complexities. To detect, interpret, and reproduce a cell change, we’ll use sets of updated published data to forward and reverse engineer these complexities starting and ending with the basic elements of a cell change. A simple change consists of varying the value of a single part (morphological or biochemical) whereas a complex change varies the values of two connected parts (data pair ratios). A cell can be in the process of changing (working out the solution) or it can be changed (problem solved). By putting the simple parts in an adaptability layer and the complex ones in a rules layer, the complexity of a cell change becomes easier to sort out. When in the process of solving a problem, a cell uses both simple and complex changes, but when the problem is solved, the simple changes may continue but the complex changes (in data pair ratios) stop (remain constant). The results (constant data pair ratios) are reproducible across publications and the value of one part automatically predicts the value of the other (a cardinal principle of classical entanglement). The table below summarizes the basics of a complex cell change.

A definition will help. When cells change, the values of individual parts change in the adaptability layer, whereas the data pair ratios in the rules layer may or may not change. This arrangement is necessary because the ratios of the rules layer establish uniformity (shared order) within and across species while changes in the adaptability layer can be highly variable according to the state of the individual (e.g., size, age, health, nutrition). While reproducibility occurs routinely in the rules layer (within and across individuals), it rarely occurs in the adaptability layer (across individuals). When a cell has changed (found the rules needed to solve a problem), the ratios no longer change but the individual parts in the adaptability layer can continue to change by adhering to the rules of the solution. These properties of single and paired parts define the complexity of a cell change in keeping with the first principles of biology. This explains why detecting and interpreting a complex cell change cannot be reduced to detecting a significant difference between two simple parts. However, detecting simple changes in single parts (morphological or biochemical) becomes possible by removing the competing changes produced by the methods.
The phenotype model harmonizes the parts, ratios, and types of changes by forward and reverse engineering the complexity of a cell change. A cell phenotype consists of nested sets of complexities beginning with relationships of structure to function, which are defined as units (U) of marker enzyme activity related to stereological estimates for membrane surface area (S) and expressed as an enzyme density (ED), wherein ED = U/S. By forming a data pair ratio from two different enzyme densities, the cell can change the ratio of the two parts (EDs) by “tuning” the amounts of the enzyme activities (U) and membrane surface (S) area(s) to produce solutions to sets of data pair ratios that appear as specific subgroups in the changed cell. Collectively, these subgroups define the solution (the changed cell) as a recipe consisting of enzyme density ratios. The figure below shows four enzyme densities: ED(A) → ED(D) arranged into two configurations of data pair ratios [ED(A)-ED(B), ED(C)-ED(D)] and displaying two states, changing (nonparallel – ED(A)-ED(B) Days 1 to 4) and changed (parallel– ED(A)-ED(B) Days 4 to 5); changing (nonparallel – ED(C)-ED(D) Days 1 to 3.5) and changed (parallel– ED(C)-ED(D) Days 3.5 to 5).
When reverse engineered, the changes in the ratios of each subgroup become apparent.

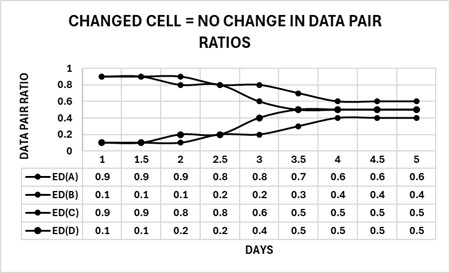
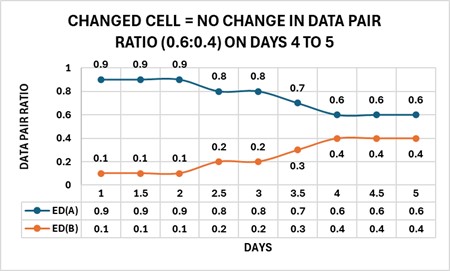
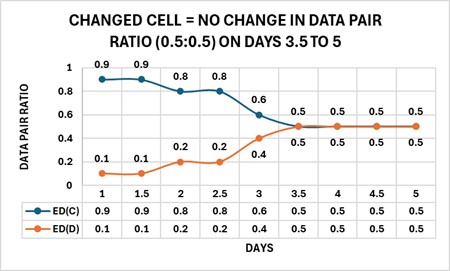
The phenotype model for cell change operates as a set of interconnected complexities. Biochemistry and morphology begin the complexity by connecting two simple parts to form an enzyme density (ED), two EDs connect to form a data pair ratio, data pair ratios sharing a similar solution form a subgroup, and several subgroups form a phenotype. Since a change starts with individual parts (morphological and biochemical) by redefining relationships of structure to function, the change model uses the enzyme density (function per structure) to define the parts used to generate the complex data pair ratios (the rules). This creates a situation wherein the cells can change the rules of the data pair ratios by dialing in the amounts (up or down) of the structural and/or functional parts of an enzyme density. By altering relationships of structure to function, the changing cell uses its simple parts to generate a series of interconnected complexities: simple parts → enzyme densities (ED) → data pair ratios → subgroups → new cell phenotype. Although it takes many enzyme densities, data pair ratios, and subgroups to define the enzyme-membrane recipe of a changed cell, the complexity of the outcome can be verified by reproducing results empirically – both before and after reverse engineering the change. In publications, however, these complex cell changes are hidden by the changes produced by the experimental methods.

Change is the key to understanding how cells work. By copying the way cells solve problems, we can learn the rules of the game and apply a first principles approach to work out how cells change. Consider the alternative. If we can’t do cell change, we can’t do reproducibility, if we can’t do reproducibility, we can’t derive biology from first principles empirically, if we can’t derive biology from first principles empirically, then we must do it theoretically. However, the theoretical approach becomes a heavy lift if the mathematics of the cells is far more advanced than ours. If, for example, cells run quantum computers and use exotic math based on both classical and quantum mechanics, then an empirical approach – at least in the short term – becomes a workable strategy.

Summary: Cells consist of two “simple” sets of parts (morphological and biochemical). We’ll use stereological estimates for the membrane surface (S) areas of organelles for the morphology and units of marker enzyme activities (U) for the biochemistry. Since the recipe of a cell phenotype exists as relationships of biochemistry to morphology, it can be expressed quantitatively – in keeping with the postulates of biochemical homogeneity – as a set of enzyme densities (ED = U/S).

Updating published data by reproducing the way cells change as complexities offers a plan B with the following list of properties.

1. Individual parts (morphological and biochemical) change.
2. Enzyme densities change.
3. Cells adjust the amounts of membranes and enzyme activities to “tune” the EDs.
4. Data pair ratios of connected enzyme densities change.
5. Changes in data pair ratios change the cell recipe at each time point.
6. A cell change occurs when the data pair ratios no longer change (for ≥ three days).
7. When the data pair ratios stop changing, the individual parts can continue to change.
8. Sets of data pair ratios (two connected EDs) expressed as polynomial curves quantify the cell changes and solutions.
9. Reverse engineering a set of polynomial curves unpacks the complexity into subgroups.
10. Each subgroup displays changes with a single solution (unique & persistent data pair ratio).
11. Cells use subgroups to triage solutions (critical EDs are solved first) .
12. In combination, the subgroups define the solution as a single enzyme-membrane recipe.
13. Links existing between subgroups can also change as part of the solution.
14. Changes in each subgroup unfold (reverse engineer) down to the original enzyme densities.