Chapter 1 – Complexity
Biology creates complexity by embedding complexity in complexity, a process that begins with molecules and spreads throughout the organism hierarchically.
But how do we solve something as complex as biology? The most efficient approach involves deriving biology from first principles, the way biology does. For us, this means capturing biology’s rules empirically from the literature with equations.
Although such rules are readily apparent in a pristine biology, they quickly disappear when we reduce biology – as we must – to a pile of disconnected parts. Consequently, solving biology consists of putting biology back together and recovering rules. In turn, the rules deliver the principles and solutions.
There is, however, a small problem. Our access to these rules comes not from a pristine biology but from an imperfect surrogate, the biology literature. Unwittingly, our experimental methods add uncertainty to our studies, which limits what we can see and do. This means that we see biology not as it exists but as we think it exists. But how do we compensate for this limitation?
We can turn to biology for help by copying its theory structure. This process consists of finding clues in the literature that we can follow to discover biology’s rules and first principles. A primer is needed because it explains how to do it. Recall that a primer is a little book of instruction written for beginners. It makes difficult things easier to understand. Solving biology – like most things – is not very difficult once you know how to do it.
The primer explains how to navigate safely across six levels of biological complexity, which include the following:
1. Patterns
2. Biochemical Homogeneity
3. Organelle Changes
4. Rate of Change
5. Cell Changes
6. Organ Changes
Chapter 2 – Equations
Capturing biology’s rules with equations allows us to communicate with biology mathematically. We ask biology a question by giving it a problem to solve by way of an experiment. In turn, biology prepares an answer by tweaking its rules to solve the problem we created. If biology repeatedly applies the same general rule under different circumstances, it becomes a candidate for a first principle.
Let’s look at a few examples of first principles.
First Principle: Biology operates its business with ratios, relating one part to another quantitatively:
x:y:z…n
First Principle: Biology defines biochemical homogeneity mathematically in two-dimensional space:
f(x)=mx
First Principle: Biology uses three spatial dimensions (0, 1, and 2) to define a change:
f(x)=mx+b
But why do these three expressions qualify as 1st principles? Because they cannot be reduced further.
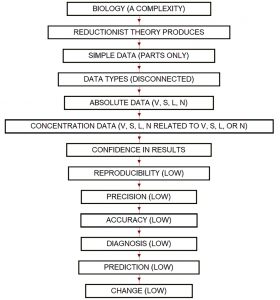
If biological complexity is based on such simple expressions, why isn’t this fact already widely known? As a science, biology currently operates under the same theory structure as physics and chemistry. It’s called reductionism. For biology, which operates as a complex adaptive system, reductionism is not the theory of choice because its purpose is to decrease or eliminate complexity.
By simplifying biology, we tacitly agree to throwing away its complexity, along with most of its rules and first principles. We fail to see a pristine biology because it no longer exists. The primer explains how to claw back the complexity, rules and first principles.
Chapter 3 – Visualizing Complexity
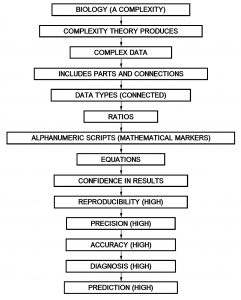
Advanced technologies simplify the task of capturing patterns, rules, equations, and first principles. For example, we can use the first level of complexity (i.e., patterns) to generate large homogeneous data sets capable of diagnosing complex disorders such as those found in the human brain. This requires translating the reduced data of research papers back into complex data types called mathematical markers and connection ratios.
The following table summarizes a data cage database. It’s populated with unique mathematical markers for 26 brain disorders and designed to deliver the correct diagnosis 100% of the time.
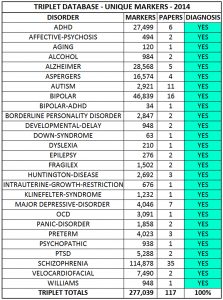
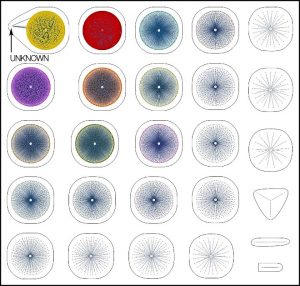
To test the effectiveness of the data cage visually, we can select twenty markers for the bipolar disorder, relabel them as unknowns, and then use the database to diagnose the unknowns. As expected, all the unknown markers are identified as belonging to the bipolar disorder.
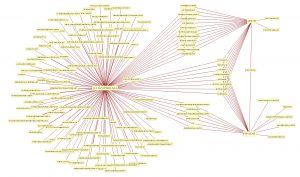
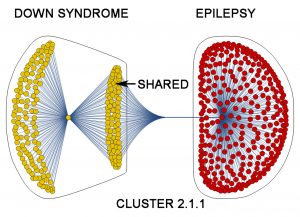
By looking for patterns created by mathematical markers with cluster analysis, we can begin to understand the relationship of one disorder to another. For example, schizophrenia shares many of its abnormal markers with other disorders, whereas Down Syndrome shares about half of its abnormal markers with epilepsy.
Chapter 4 – Reproducibility
We have two approaches to demonstrating reproducibility, our way and biology’s. Unfortunately, our way is currently under attack because it feeds a crisis of confidence in our experimental methods. How might we resolve this bewildering problem?
Starting with the same original data set, we can look for reproducibility our way (with statistics) and biology’s way (with rules). This generates two different answers, one far more interesting than the other.
Question: Do the data displayed in the figure below, which include 61 MRI estimates for the volume of the amygdala, demonstrate reproducibility across studies?
Answer: No. In fact, many of the data points would appear to be statistically different.
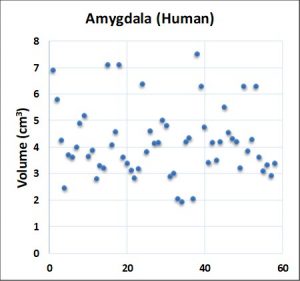
Now let’s ask biology.
Question: Is the human amygdala reproducible?
Answer: Yes. Biology solved this reproducibility problem by applying what amounts to a ratio rule (x:y:z:…n). The 61 estimates for the amygdala are in fact highly reproducible (all the MRI data detected the same left to right volume ratio – 4 (left):5(right)).
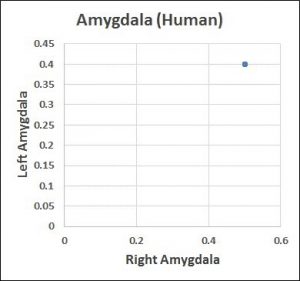
The primer explains why we’re currently suffering a reproducibility crisis and what we can do about it. By copying the way biology does reproducibility, the crisis quickly goes away.
In fact, biology is so good at enforcing reproducibility, that the primer routinely uses rule-based equations to predict and verify outcomes. Since reproducibility is fundamental to the success of a science, the primer will argue that it should be an essential part of its theory structure.
Chapter 5 – Data
In biology, we can identify two types of data: simple and complex. Simple data supply simple answers, whereas complex data supply complex answers.
For a complexity such as biology, all questions and answers exist somewhere between complex and whatever comes after complex. Our current reductionist approach to experimental biology runs largely on simple data types (zero-dimensional data points), which are information poor. This severely limits out ability to deliver reliable and reproducible results. The primer explains why.
In contrast, complexity theory provides access to complex data types (n-dimensional) that can track biological changes and allow us to scale the dimensional ladder from zero dimensional points up to one-dimensional lines and two-dimensional planes. Each increase in dimension increases the complexity and holding capacity (richness) of the data.
Chapter 6 – Databases
Databases fuel complexity theory by becoming surrogate complexities running parallel to biology. The primer uses two literature databases, one populated with stereological data and the other with MRI data. From these two starting points, we can generate a host of derivative databases – each charged with a specific task.
The primary stereology database uses a hierarchical design extending from genes to organisms, whereas the primary MRI database deals exclusively with the volumes of brain parts.
When translated into mathematical markers and connection ratios, for example, the primary MRI database uncovers widespread reproducibility in the clinical literature, as shown in the image below. Since complex data types allow us to phenotype the brain quantitatively in health and disease, we can address a wide range of unsolved problems in the basic and clinical sciences.
Chapter 7 – Calculations
For each level of complexity, sample calculations serve to demonstrate how we can use complexity theory to interact with the biomedical literature. For example, we’ll combine published data from several studies to describe a biological change by following it with and without complexity. As the analysis unfolds, we’ll see firsthand the effectiveness of a first principles approach as we extract biology’s rules from the literature. Along the way, we’ll ask challenging questions and understand why we can or cannot answer them.
REDUCTIONISM (without biological complexity)
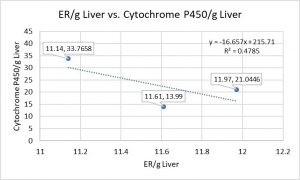
Question: Can we find a biological rule describing a quantitative relationship of structure to function?
Answer: No, the equation (R^2 = 0.4785) without an R^2 = 1 or ≈ 1 fails to detect the rule and its underlying first principle.
COMPLEXITY THEORY (with biological complexity)
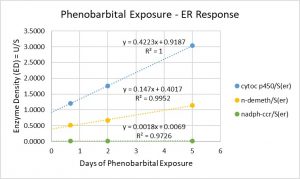
Question: Can we find a biological rule describing a quantitative relationship of structure to function?
Answer: Yes, the equations have R^2s = 1 or ≈ 1 (R^2 = 1.0000, R^2 = 0.9952, R^2 = 0.9725) and detect the rules (identified by the three equations) and the underlying first principle (f(x)=mx+b).
Chapter 8 – How to solve biology
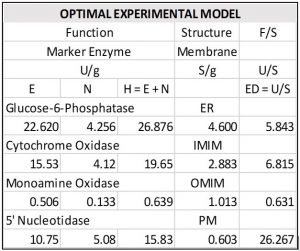
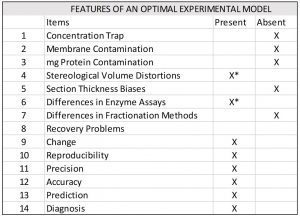
Taking our lead from genetics and molecular biology, we’ll assemble mashups and learn how to use them to solve phenotypes. This approach involves learning how to optimize our experimental models by relying on the inherent strengths of our theory structure. But what constitutes an optimal experimental model? It’s the same one that biology uses to optimize its relationships of structure to function.
The model shown below, for example, optimizes results while minimizing costs. It addresses a fundamental problem of our current experimental model.
Typically, the experimental variables we choose to follow in an experiment are swimming in a sea of unaccounted for variables that create all kinds of mischief. In short, an optimized model manages these “rogue” variables within the context of a complexity model.
Chapter 9 – Complexity theory
Complexity theory states that it takes a complexity to solve a complexity. Since the theory comes from biology, it offers a robust way to discover, understand, and innovate. Complexity theory works because it’s copied from biology.
Consider, for example, the way in which biology changes a cytoplasmic membrane in response to a threat. As shown in the figure below, it instigates a change by applying two basic principles – both of which define relationships of structure to function. Notice what happens. During a biological change, complexity develops step-wise as it spreads across distinct levels of the biological hierarchy. In fact, a biological change involves so many complex events and interactions that it can only be captured and interpreted with equations.
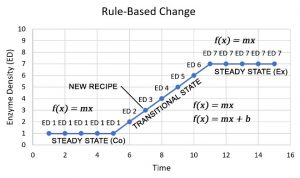
The Point? Without help from biology, we discover chaos. With help, we discover order.